拉巴力的纸皮箱

LayerNorm：从“为什么要归一化”到“为什么 Transformer 离不开它”

发表于 2026-02-02

以下内容由AI辅助生成

神经网络训练的过程，看起来是在“学习语义”或“理解结构”，但在更底层，它其实是一件非常朴素的事情：
一层一层地传递和变换数字。

而几乎所有训练不稳定、梯度异常、不收敛的问题，最终都可以归结为一个原因：

中间数值的尺度失控了。

LayerNorm（Layer Normalization）正是为了解决这个问题而出现的。但要真正理解它，不能从公式开始，而必须先回到一个更基础的问题：什么是归一化，神经网络为什么需要归一化。

一、什么是“归一化”：先抛开神经网络

先从一个生活中的例子出发。

假设你要比较两次考试成绩：

一次考试满分 150
另一次考试满分 100

你不能直接比较 120 分和 80 分谁更好，因为它们的尺度不同。

一个更合理的做法是：

减去平均值
再除以标准差

这样得到的数值不再依赖原始分数范围，而只反映相对水平——平均值约为 0，波动程度约为 1。

这就是归一化（Normalization）的本质思想：

不改变相对差异，只统一数值尺度。

二、神经网络为什么必须做归一化

回到神经网络。神经网络的基本操作是反复进行线性变换：

如果输入的尺度稍微偏大，权重没有被精细约束，那么输出很容易比更大或更小。

当层数不断增加时：

1	x → y → z → u → …

哪怕每一层只“放大或缩小一点点”，结果也会变成：

激活值越来越大（数值爆炸）
或越来越小（数值消失）

这就像一张图片被反复复印：复印次数一多，画面一定会失真。

于是，一个非常直接但极其重要的工程直觉出现了：

能不能在每一层之间，把数值拉回到一个“正常范围”？

这正是神经网络中各种 Normalization 方法存在的根源。

三、LayerNorm 到底在归一化什么

在 Transformer 中，每个 token 在某一层都会被表示成一个向量：

这个数一起，构成了模型在当前层对这个 token 的全部状态描述。

LayerNorm 的做法非常明确：

不看其他 token
不看 batch
只对当前这个 token 自己的向量做归一化

具体来说，它会在特征维度（hidden dimension）上计算均值和方差：

然后进行标准化，并加上可学习的缩放与平移参数：

归一化之后，向量的均值约为 0、方差约为 1，但通过和，模型仍然可以学习合适的尺度。

一句话总结：

LayerNorm 是对“每一个 token 自己的向量”做归一化，完全不依赖其他 token 或 batch。

四、为什么 Transformer 特别容易“数值失控”

理解了归一化之后，再看 Transformer 的结构，就会发现：它在数值层面上，天然是一个不稳定系统。

原因来自三个叠加的结构性因素：

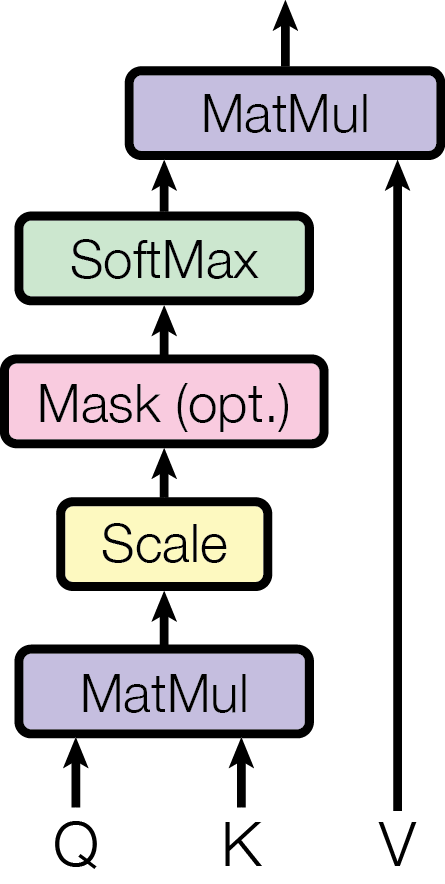
1. Attention 是不受约束的加权求和

Attention 的输出形式是：

它本质上是多个向量的线性组合，目标是混合信息，而不是控制输出尺度。缺少约束时，某些 head 的输出可能越来越大，某些维度可能长期主导，不同 token 的数值分布会逐渐漂移。

2. 残差连接会层层累加数值

Transformer 中每一层都有残差结构：

残差的作用是保证信息通路，但它也意味着新信息会不断叠加到旧表示上，数值会随着层数持续累积。

一个常见的误解是把 residual 当作“稳定器”。更准确的说法是：

Residual 负责信息通路，但并不负责数值稳定。

3. Softmax 对尺度极其敏感

Attention 内部使用 softmax，而 softmax 只在一个很窄的数值区间内工作得好：

输入过大 → 接近 one-hot → 梯度几乎为 0
输入过小 → 接近均匀分布 → 注意力失效

Transformer 同时包含 Attention 的加权求和、Residual 的数值累加、Softmax 的高敏感性——如果没有归一化，数值失控几乎是必然的结果。

五、LayerNorm 如何“救场”

LayerNorm 的作用可以概括为一句话：

在每一层，把每个 token 的表示拉回到同一个稳定的统计坐标系。

它在 Transformer 中的分工可以用这张图来理解：

输入 token 向量 x
        |
        v
   [ Attention ]        <- 看别人：混合信息
        |
        v
      f(x)
        |
        +-------------------+
        |                   |
        v                   |
   [ Residual: x + f(x) ]   <- 保自己：信息不断
        |
        v
   [ LayerNorm ]            <- 稳自己：归一化、控数值
        |
        v
     交给下一层

三者的职责是：

Attention 管信息交流
Residual 管信息传承
LayerNorm 管数值纪律

LayerNorm 带来的直接效果包括：

各层输入分布保持相对一致
数值不再随层数漂移
softmax 始终工作在有效区间
梯度能够稳定传播

因此可以说：

没有 LayerNorm，Transformer 在数学上是一个不稳定系统；有了 LayerNorm，它才成为可训练的深层模型。

六、为什么不用 BatchNorm

在讨论 LayerNorm 时，BatchNorm 经常被拿来对比。它们同属“归一化家族”，但适用场景完全不同。

BatchNorm 的核心思想是：

利用一个 batch 内所有样本的统计量来做归一化。

这在 CNN 中非常合理（输入尺寸固定、batch 结构稳定），但在 Transformer / NLP 中，会遇到根本性冲突：

1. Batch 本身不稳定

句子长短不同
padding 复杂
推理时常常 batch = 1

2. Token 不应被迫参考其他样本

Transformer 的设计是让 token 之间的交互只发生在 Attention 中，归一化阶段不应引入额外耦合。而 BatchNorm 恰恰会让一个 token 的数值受其他 token、其他样本影响。

LayerNorm 则完全相反：不看 batch、不看其他 token，只对自身状态做校准。

一句话总结区别：

BatchNorm 在“群体里”找尺度，LayerNorm 对“自己”做校准。

Transformer 需要的是后者。

结语：把 LayerNorm 放回正确的位置

LayerNorm 并不是 Transformer 的“附加技巧”，而是归一化思想在序列建模中的一次精准落地：

以 token 为基本单位
不依赖 batch
不混淆语义交互与数值校准

它让 Transformer 能在极深的结构中，始终保持数值可控、梯度可传、注意力可学习。

Transformer 架构笔记：组件、机制与设计思路

发表于 2026-02-02

以下内容由AI辅助生成

引言：三个核心抽象

在理解 Transformer 之前,可以先记住三句话：

Attention = 状态之间的信息路由
FFN = 状态内部的非线性变换
Multi-Head = 多种关系子空间的并行建模

这三句话不是对 Transformer 的技巧性总结,而是对其核心思想的抽象表达。它们并非 Transformer 独有的新概念,而是长期存在于神经网络中的通用思想,在 Transformer 中被系统化、模块化、工程化地组织在了一起。

Transformer 的重要性不在于它「发明了什么全新的思想」,而在于它第一次把信息如何流动和状态如何更新这两件事彻底解耦,并用统一、可扩展的结构反复堆叠,从而构建出今天的大模型体系。

整体架构概览

输入序列: [x₁, x₂, ..., xₙ]
    ↓
[Token Embedding + Position Encoding]
    ↓
┌─────────────────────────────────────┐
│     Transformer Block (×N层)        │
│  ┌───────────────────────────────┐  │
│  │   Multi-Head Self-Attention   │  │
│  │   (信息路由：谁和谁交互)         │  │
│  └───────────────────────────────┘  │
│             ↓                       │
│      [Residual + LayerNorm]         │
│             ↓                       │
│  ┌───────────────────────────────┐  │
│  │  Feed-Forward Network (FFN)   │  │
│  │  (信息变换：交互后如何变化)       │  │
│  └───────────────────────────────┘  │
│             ↓                       │
│      [Residual + LayerNorm]         │
└─────────────────────────────────────┘
    ↓
[LM Head: 映射到词表]
    ↓
输出概率分布

上图展示了 Transformer 的整体数据流：输入经过 embedding 和位置编码后,通过 N 层相同的 Block 进行处理。每个 Block 包含两个核心组件（Attention 和 FFN）,以及用于稳定训练的残差连接和归一化。下文将逐一展开这些组件的细节。

一、Transformer 解决什么问题？

Transformer 是一种序列建模架构。它的输入和输出本质上都是 token 序列,目标是学习如下形式的函数：

其中最大的困难只有一个：

每个位置的表示,既要知道其他位置的信息,又要知道自己该如何变化。

Transformer 对这个问题的解决方案：

用 Attention 解决「谁和谁交互」
用 FFN 解决「交互之后如何变化」

这构成了 Transformer 的第一性原理。

更进一步看,Transformer 用纯 Attention 结构解决了序列建模的并行性和长距离依赖问题,也是现代大模型的结构源头：

并行性主要由 Self-Attention 机制 解决
长距离依赖主要由 Self-Attention + 多头机制 + 结构设计 共同解决

并行性是怎么解决的？

核心在于 Self-Attention + 去掉 RNN/CNN：

Self-Attention 对整个序列做矩阵运算
所有 token 同时计算
不再有时间步依赖
训练从 O(n) 串行 → O(1) 层级并行

长距离依赖是怎么解决的？

靠 Self-Attention 为核心的一组组件协作完成：

Self-Attention：任意两个位置一步直连
Multi-Head Attention：不同 head 专门学不同远程关系
Residual + LayerNorm：远程信息和梯度不易消失
Positional Encoding：让“远近”有意义

一句话总括：Self-Attention 让所有位置直接互相看到,从而同时解决并行计算和长距离依赖问题。

二、输入不是「文字」,而是状态向量

1. Token 与 Tokenizer

模型不直接处理字符或词语,而是处理 token。输入文本首先经过 tokenizer,被切分为 token_id 序列。

现代 tokenizer 采用子词或字节级策略（BPE、WordPiece、Unigram、Byte-level BPE）,核心原则是：

任何输入字符最终都能被表示成 token_id 序列。

即使遇到生僻文字或罕见字符,tokenizer 也不会「找不到词表」,而是退化为更细粒度的子词甚至 UTF-8 字节表示（代价是 token 数变多）。

词表中允许存在重叠 token（如「我 / 非常 / 喜欢 / 非常喜欢」同时存在）,但一次分词只选择一条最优切分路径,不产生冗余。

2. Token Embedding

token_id 通过 embedding 矩阵映射为向量：

1	token_id → embedding ∈ R^d

三个关键事实：

token_id 是固定的索引
embedding 向量是可训练参数
embedding 的具体值在训练过程中不断学习更新

embedding 不是人为定义的语义,而是完全数据驱动学出来的状态表示。

3. 位置编码：为什么必须有？

Attention 的核心计算基于内容相似度,本身不关心顺序。如果不引入位置信息：

「我喜欢你」与「你喜欢我」在 Attention 看来只是同一组 token 的不同排列。

这在数学上对应 Attention 的置换等变性（Permutation Equivariance）：重排输入只会导致输出对应重排,不会产生「顺序语义」。

但语言、时间序列、音频、代码都是顺序敏感的,因此必须引入位置信息。

常见方式：

可训练的位置 embedding
正弦位置编码
RoPE、ALiBi 等相对位置机制

需要特别指出：

位置编码在训练和推理中都参与 forward 计算
只是有些实现把位置作为参数存储,有些作为计算规则存在

位置编码不是「知识」,而是 Transformer 理解序列的坐标系。

三、Attention：可学习的信息路由机制

1. Q / K / V 的定义

给定某一层的输入状态：

关键点：

是参数矩阵
对所有 token 共享
Q / K / V 是运行时动态计算的

模型不保存「每个 token 的 Q/K/V 表」,而是保存「如何从任意状态映射到 Q/K/V 的规则」。

核心理解：

Q / K / V 本质是同一个 token 在不同「视角空间」的表示。

Attention 的计算过程 = 用 Query 空间去 Key 空间里做相似度搜索,再把 Value 空间的信息加权汇总。

从语义角色看：

Query：查询目标（「我在找什么」）
Key：匹配索引（「我能被什么找到」）
Value：传递信息（「我要传递什么内容」）

这是典型的内容寻址（content-based addressing）。

为什么要分离 Q / K / V？

如果用同一向量同时表示「查询需求」「匹配标识」「传递内容」,会导致：

表达能力受限：查找规则和信息内容被绑定
优化困难：一个维度的变化同时影响三种语义角色
学习粗糙：无法独立学习不同的关系模式

分离后的优势：

解耦需求与内容：不同维度专门用于「问问题」（Q）、「当索引」（K）、「装内容」（V）
更高表达自由度：使 Attention 从简单的「相似度混合」升级为「可学习的信息检索」
稳定的优化路径：三个投影矩阵可独立学习

2. Attention 的计算公式

这一过程：

用 Q 和所有 K 做相似度匹配
softmax 得到注意力权重分配
对 V 做加权求和完成信息汇聚

这正是「状态之间的信息路由」。

公式背后的设计逻辑

为什么是（点积）？

点积计算向量相似度：

score[i, j] = Q_i · K_j^T
            = Σ (d = 1 → d_k) Q[i, d] × K[j, d]

若和方向一致（需求匹配）,点积大
若方向不一致,点积小甚至为负
点积满足：可微、高效（GPU 友好）、在高维空间稳定

这是典型的基于内容的相似度匹配。

为什么除以？

这是数值稳定性问题。当维度很大时：

点积的方差随维度线性增长
导致 softmax 输入值过大,迅速饱和
梯度接近 0,难以训练

通过缩放,将数值分布控制在合理范围。

为什么用 softmax？

softmax 提供三个关键性质：

所有权重 ≥ 0
所有权重和 = 1（归一化的概率分布）
可微且梯度稳定

这使注意力权重具有明确的概率解释：「当前 token 有 60% 在看 A,30% 在看 B,10% 在看 C」。

为什么最后乘 V？

因为只决定看谁、看多少,而决定拿什么内容。最终输出是加权信息汇聚：

1	output[i] = Σ_j α[i, j] · V[j]

其中是归一化后的注意力权重。

3. Self-Attention 与 Cross-Attention

Self-Attention 的定义

Self-Attention 的核心特征：Q、K、V 都来自同一条序列（同一组状态）。

这里是同一序列的隐状态。即：

同一批 token
既提问（Query）
又被提问（Key）
又提供信息（Value）

可理解为：序列「对自己」做 Attention,是序列内部的信息路由与整合。

Cross-Attention（交叉注意力）

在 Encoder-Decoder 架构中：

Query 来自 Decoder
Key 和 Value 来自 Encoder

这是 Decoder 「对 Encoder 做 Attention」,用于对齐两个不同序列。

对比总结

类型	Q 来源	K/V 来源	用途
Self-Attention	同一序列	同一序列	序列内部信息整合
Cross-Attention	Decoder	Encoder	跨序列信息对齐
Masked Self-Attention	同一序列	同一序列（带因果 mask）	自回归生成

Self-Attention 的设计意义

Transformer 选择 Self-Attention 作为核心机制,有三个关键优势：

打破顺序依赖：不像 RNN 需要逐步处理,可全局并行计算
任意两点直接交互：第 1 个 token 可直接关注第 1000 个 token,路径长度为 1
对称、通用、可扩展：不假设语法结构、不假设距离关系,所有结构由数据驱动学习

核心直觉：

可把序列想象成一群人在讨论：

每个人既听别人说话,又被别人听
没有「外部信息源」,所有信息都在这群人之间流动
这就是「Self」的含义——序列内部的自我关联

Masked Self-Attention

Decoder 中使用的 Masked Self-Attention 仍是 Self-Attention,只是增加了约束：

每个位置只能看到之前的位置（因果 mask）
但 Q、K、V 依然来自同一序列

因此：Masked Self-Attention = 带因果约束的 Self-Attention

四、Multi-Head：并行的关系子空间

基本原理

Multi-Head Attention 不是「多算几次同样的 Attention」,而是：

每个 head 有自己的
从同一输入状态投影到不同子空间
在不同子空间中学习不同关系模式

实现上通常把划分为多个 head 的维度并行计算,最后拼接,并通过线性矩阵融合。

子空间的具体实现

假设 ,,则每个 head 的维度。

实现方式（不是 8 套完全独立的小 Attention）：

一次性线性投影：
Reshape：,分配给 8 个 head
每个 head 独立计算 Attention
Concat + 融合

「子空间」的含义：

不是人工预先指定的「语法子空间」或「语义子空间」
而是：同一输入在不同线性投影下,被映射到不同方向的表示空间
每个 head 有独立的 ,天然定义了不同子空间

的关键作用

为什么不能直接 concat？

因为：

每个 head 只在低维子空间中工作
concat 只是简单拼接,不同 head 之间没有交互
缺少信息融合机制

的本质作用：

信息融合：把多个 head 的结果线性混合,允许 head 之间交互
维度映射：将拼接后的向量映射回 ,以便与残差连接相加
输出投影：作为 Attention 层真正的「输出投影层」

可将理解为「多头专家讨论结束后的总编辑」。

为什么每一层都要自己的？

因为不同层关注的关系层级不同：

底层：偏局部、句法关系
高层：偏语义、抽象关系

每一层的「信息融合方式」应该不同,所以每层都有独立的参数。

不同 Head 如何实现分化？

Multi-Head Attention 没有显式的互斥机制来强制不同 head 学习不同模式。那为什么它们通常不会学成完全一样？

三种隐式分化机制

1. 参数初始化的差异

每个 head 的初始值不同,导致：

优化轨迹不同
早期梯度方向不同
进入不同的局部最优区域

2. 路径依赖的梯度更新（核心机制）

这是最关键的分化压力：

每个 head 接收到的梯度,取决于它当前「已经在关注什么」
一旦 head 之间产生微小差异,梯度会放大这种差异,而非抹平
优化是路径依赖的：不同的 attention pattern → 不同的梯度信号 → 进一步分化

例如,即使两个 head 都偏向「长距离依赖」,它们可能分别专注于：

head A：句法长距离（主语-谓语跨句）
head B：指代长距离（代词-先行词）

Attention pattern 不同 → 对 loss 的贡献路径不同 → 梯度方向不同 → 继续分化

3. 带来的隐式竞争

所有 head 的输出最终通过融合,这产生资源竞争机制：

模型的最终 loss 只关心「哪些 head 的信息真的有用」
若两个 head 提供高度相似的信息,对 loss 的边际贡献是冗余的
梯度会倾向于：强化其中一个,让另一个转向其他有用方向
这是隐式的多样性压力：冗余 head 是「浪费参数」,优化倾向于减少浪费

Head 分化的实际表现

在训练好的语言模型中,常见现象：

某些 head 专注局部依赖（相邻 token）
某些 head 专注长距离依赖
某些 head 偏向句法关系（主谓宾）
某些 head 偏向指代关系（he/she/it）

没有任何硬编码规则,这些模式都是训练自发形成的。

Head 冗余现象与过参数化设计

需要指出：Multi-Head Attention 确实会出现冗余。

已知现象：

多个 head 可能学到非常相似的 attention pattern
某些 head 几乎「没在干活」
Head 利用率不均

实验证据：

论文表明：可剪掉相当一部分 head,性能几乎不变
Head pruning（头剪枝）后的模型：参数更少、推理更快、性能基本不降

这说明：Multi-Head Attention 在实践中是过参数化的。

为什么接受过参数化？

过参数化是特性,不是 bug
- 让优化更容易
- 给模型更多「自组织」的自由度
- 降低了设计者必须「手工指定结构」的需求
显式互斥约束反而可能伤性能
- 历史上有人尝试过：强制 head 正交、去相关 loss、specialization 正则项
- 结果往往是：训练更难、收敛更慢、泛化未必更好
- 原因：模型「知道自己该怎么分工」,人为强行规定反而限制了自由度

核心理解

Multi-Head Attention 是一种「软分工、自发组织」的机制：

没有显式互斥机制来防止多个 head 学到相似模式
通过参数初始化差异、路径依赖的梯度更新、输出融合层的隐式竞争,在实践中形成自发分工
这种结构是刻意过参数化的,允许一定程度的冗余,而非强制最优分解
Head 数量（8、16、32、64）是超参数,代表并行关系建模的容量上限,而非「关系类型数」

五、FFN：状态内部的非线性变换

Attention 完成了「信息路由」——决定了从哪里汇聚信息。但汇聚后的信息如何变换？这就是 FFN 的职责。

FFN 的结构

核心特征：

逐 token 计算：对序列中每个 token 独立应用同一套参数
参数共享：所有位置使用相同的
无交互性：token 之间不发生信息交换
强非线性：通过激活函数引入非线性变换
升维-压缩：通常先升维（如 4×d）再降维

典型配置：

（升维,通常）
（降维）
：激活函数（ReLU、GELU、SwiGLU 等）

为什么 Attention 本身不够？

Attention 的核心输出是：

这是线性加权和。即使注意力权重通过 softmax 非线性计算,但对的操作仍是线性的。

线性操作的局限：

不能创造新特征
不能做复杂的特征组合
不能实现条件逻辑（「A 且 B」这类组合）

深度学习的基本原理：没有非线性,深度网络再深也等价于一个线性变换。

FFN 为什么能「重塑表示」？

1. 非线性激活打破线性限制

激活函数引入了真正的非线性,使模型能够学习复杂的非线性函数。

2. 升维 → 非线性 → 压缩 = 特征重组

可将 FFN 理解为：

展开：将 token 表示投影到高维空间（）
变换：在高维空间进行非线性「切割」和「门控」
压缩：再投影回原空间（）

这允许模型学到：

高阶特征组合：复杂的特征交互模式
条件激活：某些特征只在特定上下文中生效
抽象语义方向：更高层次的语义表示

Attention 与 FFN 的分工

这两个组件在 Transformer 中扮演互补角色：

Attention：负责「关系建模」
- token 之间可以交互
- 决定「看谁」
- 完成信息汇聚
FFN：负责「表达变换」
- token 之间不交互
- 决定「变成什么」
- 完成信息重组

直观比喻：

把序列想象成一排学生：

Attention 阶段：学生之间讨论、互相参考答案
FFN 阶段：每个学生回到座位,用同一套规则独立思考

没有学生和旁边的人交流,但大家使用的是同一本「公式书」（共享参数）。

「逐 token」的精确含义

关键点：FFN 不让 token 之间交互。

如果有序列 ,FFN 的计算是：

特征：

✔ 每个 token 独立计算
✔ 参数共享（同一套）
✔ 可完全并行（所有 token 同时计算）
❌ token 之间 无信息交换

这种设计有三个优势：

解耦职责：Attention 专注关系,FFN 专注变换
高效并行：所有位置可同时计算
增强非线性：每个 token 都经历完整的非线性变换

这种设计实现了关系建模与表示变换的解耦,两者各司其职又相辅相成。

如果没有 FFN 会怎样？

如果只堆叠 Attention + Residual,而没有 FFN：

整个网络退化为多次线性混合
表示空间无法被真正「变形」
模型退化成复杂的线性滤波器
表达能力严重受限,无法逼近复杂非线性函数

实验和理论都表明：FFN 是 Transformer 表达能力的关键来源。

六、Residual 与 LayerNorm：深度可训练性的关键

为了让多层堆叠可行,Transformer 使用了两项关键技术：

残差连接（Residual Connection）：防止信息退化,允许深层网络
LayerNorm：稳定数值分布,避免训练崩溃

现代模型几乎全部采用 Pre-LN 结构以增强稳定性。

这两项技术不是 Transformer 的创新,但它们对于构建深层网络至关重要。没有它们,Transformer 无法堆叠到几十层甚至上百层。

七、Transformer Block：整体架构

现在已经理解了所有核心组件,可以看看它们如何组织成完整的架构。

Block 的基本结构

无论 Encoder 还是 Decoder,Transformer 的核心都是反复堆叠同一种 Block。典型结构：

Multi-Head Self-Attention
Residual + LayerNorm
Position-wise FFN
Residual + LayerNorm

Transformer 本质就是：这个 Block 堆叠 N 次。

N 取决于模型规模,从十几层到上百层不等。

信息流动的完整路径

在每个 Block 中：

Attention 阶段：通过 Self-Attention 完成信息路由,让每个 token 从其他 token 汇聚相关信息
残差连接：保留原始信息,防止信息丢失
LayerNorm：稳定数值分布
FFN 阶段：对汇聚后的信息进行非线性变换,重塑表示
再次残差 + LayerNorm：稳定输出

这个过程反复进行 N 层,逐步抽象和精炼信息。

Encoder vs Decoder

Encoder：

可看到完整输入序列
没有因果 mask
输出的是「被充分理解后的表示」
典型应用：文本理解、分类、检索向量（BERT）

Decoder：

使用 Masked Self-Attention（因果 mask）
每个位置只能看到之前的位置
用于自回归生成
典型应用：语言模型（GPT）

Encoder-Decoder：

Decoder 中额外包含 Cross-Attention 层
用于对齐两个序列（如机器翻译）
典型应用：T5、BART

为什么大模型几乎都是 Decoder-only？

因为大模型的核心训练目标是自回归语言建模：

而互联网数据天然是连续文本流,不是严格的输入/输出对。Decoder-only：

目标函数最简单
数据利用率最高
工程实现最统一
推理与 KV Cache 高度契合

因此成为通用大模型的事实标准。

八、训练与推理：模型到底在「存什么」？

1. 模型参数存储的内容

训练完成后,模型保存的是：

token embedding 矩阵
各层的
FFN 参数（）
LayerNorm 参数
输出层参数（）

Q/K/V 本身不是参数,只是中间计算结果。

模型保存的是「规则」而非「结果」——保存的是如何计算 Q/K/V 的权重矩阵,而非每个 token 的具体 Q/K/V 值。

2. 推理过程概览

推理时,模型以自回归方式反复执行：

当前 token 序列 → forward
预测下一个 token 的概率
采样或选择 token
拼接到序列末尾
重复

上下文长度始终等于：

输入 token 数 + 已生成 token 数

hidden states 是中间变量,不算 token,不占上下文长度。

3. 完整推理流程详解

以 Decoder-only 模型（如 GPT）为例,假设当前输入序列为 [x₁, x₂, ..., xₜ]：

第 1 步：Embedding + 位置编码

得到第 0 层（输入层）的隐状态矩阵：

第 2 步：逐层 Transformer Block

对第层（）：

LayerNorm（Pre-LN）
计算 Q/K/V
Masked Self-Attention（每个位置只能看到之前的位置）
Multi-Head 融合
残差连接
FFN + 残差

第 3 步：提取最后一个 token 的表示

因为语言模型的目标是预测：

第 4 步：映射到词表（LM Head）

第 5 步：采样下一个 token

通过采样策略（greedy、top-k、top-p、temperature）得到：

第 6 步：拼接并重复

将新 token 加入序列：[x₁, x₂, ..., xₜ, x_{T+1}],然后重新执行整个 forward 过程。

关键理解：推理不是「在同一个 forward 里不断计算」,而是每次 forward 只预测一个 token,然后将其接到序列后面再完整计算一遍（或使用 KV Cache 加速）。

4. KV Cache：推理加速的关键优化

在生成第个 token 时,Attention 需要所有历史 token 的 K/V。但这些历史 K/V 在后续步骤中不会改变。

因此在推理阶段：

历史 token 的 K/V 被缓存
新 token 只需计算一次 K/V
Attention 直接使用缓存 + 新值

KV Cache 不是新结构,而是 Attention 在推理阶段的缓存优化,使生成从反复重算历史变为高效增量计算。

什么是「历史 token」？

在自回归生成中：

历史 token = 当前这一步之前,已经确定下来的所有 token

包括两部分：

最初输入的 prompt token
之前步骤中模型生成并已接纳的 token

生成过程示例

假设输入 prompt：[我, 喜欢]

第 1 步：预测第 3 个 token
- 当前序列：[我, 喜欢]
- 历史 token：[我, 喜欢]
- 它们的 K/V 被计算并缓存
- 预测出：吃
第 2 步：预测第 4 个 token
- 当前序列：[我, 喜欢, 吃]
- 历史 token：[我, 喜欢, 吃]（注意「吃」已成为历史）
- 只需为「吃」计算新的 K/V 并追加到缓存
- 预测出：苹果
第 3 步：预测第 5 个 token
- 当前序列：[我, 喜欢, 吃, 苹果]
- 历史 token：所有 4 个 token
- 只为「苹果」计算新 K/V

Token 实例 vs Token 类型

关键区分：

Token 类型（token_id）：tokenizer 层面的概念,如「我」的 token_id 可能是 1234
Token 实例（token occurrence）：序列中特定位置的 token,即使 token_id 相同,不同位置也是不同实例

为什么相同 token_id 的 K/V 也不同？

假设序列是：[我, 喜欢, 我]

两个「我」虽然 token_id 相同,但：

位置不同
$我$
$我$
上下文不同（这是更关键的原因）
- 第 1 个「我」只能看到自己
- 第 3 个「我」能看到 [我, 喜欢, 我]
- Attention 结果完全不同
因此 K/V 不同

由于 ,所以 ,

KV Cache 的精确含义

Transformer 不关心「这个 token 是否重复出现」,只关心「这是序列中的第几个位置」。

KV Cache 缓存的是：

某一层、某一 head、某一位置的 K 和 V
不是某一 token_id 的 K/V

缓存结构：[(pos=1, token=我), (pos=2, token=喜欢), (pos=3, token=我)]

每个位置都是独立的 token 实例,即使 token_id 重复。

历史 K/V 「不会改变」的含义

在推理阶段（参数固定的前提下）：

某个 token 实例一旦被计算过,它在该层的 K/V 就完全确定
后续生成步骤中不会再修改这些缓存值
新生成的 token 会计算新的 K/V 并追加到缓存中

这就是为什么 KV Cache 能大幅加速推理：避免了对历史 token 的重复计算。

九、设计哲学：演化与涌现

经过前面的技术细节,现在可以从更高层次理解 Transformer 的设计哲学。

演化而非推导

需要强调一个常被忽视的事实：

Transformer 并不是从第一性原理必然推导出的最优结构,而是在数学约束、工程约束和实验验证下,逐步演化出来的高度有效的架构。

其设计逻辑可以概括为：

目标是表达能力：所有数学结构（Attention、FFN、Multi-Head 等）共同构造一个高表达力、可优化的函数空间
训练填充能力：通过大规模数据和梯度下降,让参数收敛到该空间中能有效建模数据分布的区域
推理是涌现结果：所谓的「推理能力」不是显式编程的,而是模型在训练后自然呈现的行为模式

核心洞察

现代深度模型不是在「显式地教模型如何推理」,而是构造一个足够大、足够灵活的函数空间,让「推理能力」作为训练后的自然涌现结果出现。模型学到的是「在什么样的上下文下,下一个 token 的条件分布是什么」,而不是「如果 A 且 B,则推出 C」这样的显式逻辑规则。

这意味着：

Transformer 的各个组件共同构成一个可学习的表示空间,而非独立的「智能模块」
每个「数学技巧」（LayerNorm、Residual、缩放、softmax）本质都是在让训练能够找到好解
结构的有效性来自：表达力（能表示什么）+ 可优化性（能不能学到）+ 工程可行性（能不能实现）的综合平衡

三层架构的本质

Transformer 的成功来自三层要素的协同：

第一层：函数空间（结构设计）

Attention：决定状态如何互相连接
FFN：决定状态如何非线性变换
Multi-Head：决定并行关系容量
→ 这一层决定了「能表示什么」

第二层：优化可达性（数学与工程）

LayerNorm、Residual：稳定训练
参数初始化、缩放技巧：控制数值
自回归目标：简化优化
→ 这一层决定了「能不能学到」

第三层：数据分布（语义与行为）

语言结构、逻辑模式
世界知识、推理痕迹
人类文本中的统计规律
→ 这一层决定了「学成什么样」

关键洞察：所谓的「推理能力」不在任何一层内部,而是在三层叠加后的整体行为上自然涌现。

设计的演化本质

Transformer 的诞生过程可以理解为四重约束下的结构搜索：

可微约束：必须端到端可训练、能在 GPU 上高效计算
表达约束：必须能表示足够复杂的函数、能够 scale
工程约束：必须并行友好、易于分布式训练
实验约束：必须在当时的计算资源和数据规模下表现明显更好

这不是演绎推理的结果,而是一种受约束的经验演化过程——更像生物进化、工程设计,而非形式逻辑证明。

许多看起来「有道理」的解释,实际上是事后合理化：结构先被实验验证为有效,理论解释是在「理解为什么它能活下来」。这是典型的科学路径：先发现 → 再解释 → 再抽象 → 再指导下一轮设计。

从结构到能力的涌现

核心理念：

现代深度模型的设计,本质上不是在「显式地教模型如何推理」,而是：

构造一个高表达力、可优化的函数空间
让训练过程在大规模数据的约束下,将参数收敛到该空间中的某个有效区域
从外部观察,这种函数行为呈现出类似推理、理解与规划的能力

这意味着：

模型没有「推理模块」,它只是学到了一个在训练分布上表现得「像在推理」的函数
推理是外部观察者给出的解释,不是模型内部的显式过程
能力的涌现依赖于：结构设计允许的表达空间 × 数据分布蕴含的模式 × 优化过程能够到达的区域

结语：Transformer 的最终抽象

技术层面的总结

Transformer 是一种以 token 为单位的序列建模框架：

通过 Attention 实现可学习的全局信息路由
通过 FFN 实现逐 token 的非线性状态变换
通过多头并行建模不同关系子空间
依靠残差与归一化稳定深度训练
在 Decoder-only 形态下以自回归方式逐步生成输出
所有长期知识存于参数中,短期上下文由 token 序列动态提供

理解的三个层次

理解 Transformer,有三个层次：

技术层次：知道每个组件是什么、怎么算
原理层次：理解为什么需要这些组件、它们解决什么问题
哲学层次：认识到这些结构不是理论推导的必然,而是在约束空间中探索的产物

当开始思考「为什么是这个结构而不是别的」时,认知就从第二层进入了第三层。

这一思考过程本身就是深入理解的标志——它意味着不再将 Transformer 视为完美的理论大厦,而是理解其本质：在当前认知、资源和工程能力约束下,演化出的一条可行且有效的路径。

Transformer 的成功,本质上是：在正确的约束下,允许了正确的涌现。

从 RNN 到 Transformer:序列建模的结构性转变

发表于 2026-01-31

以下内容由AI辅助生成

一、自然语言建模的真正难点

自然语言处理的困难，并不在于单词本身，而在于单词之间如何构成有意义的整体。一句话的语义，往往由跨越较长距离、受句法和语义结构约束的成分共同决定。主语与谓语之间可能相隔多个从句，但它们之间的依赖关系依然是理解句子的关键。

因此，自然语言建模的核心问题，本质上是一个序列建模问题：模型需要在任意位置上，合理利用来自序列中其他位置的信息，尤其是那些距离较远但语义上至关重要的部分。

二、表示与结构的分离：从词向量说起

在神经网络进入 NLP 之前，单词只是离散符号，计算机无法直接处理。word2vec 等词向量模型通过分布式假设，将单词映射到连续向量空间，使语义相近的词在向量空间中彼此接近，从而为神经网络提供可计算的输入表示。

这类方法解决的是“词如何用向量表示”的问题：把离散的 token 变成可计算、可度量相似性、可组合的向量。但词向量并不理解语言结构，它不包含顺序、依赖或句法信息。在词向量层面，“dog bites man” 与 “man bites dog” 的差异极小。因此，词向量只是语言处理的表示层，而真正负责建模语言结构和依赖关系的，是后续的序列模型。

三、RNN：用状态表达序列的直觉解法

循环神经网络（RNN）是最早系统性处理序列数据的神经网络结构。它的核心思想非常直观：将序列看作一个随时间推进的过程，用一个隐藏状态不断吸收历史信息，并与当前输入共同决定下一状态。

在这一框架中，隐藏状态被视为“到目前为止的全部记忆”，序列信息被逐步压缩进一个向量中。对于较短、依赖结构简单的序列，这种机制能够有效工作。然而，在自然语言中，这一设计逐渐显露出根本性的局限。

四、编码器思想与固定长度向量的隐患

在 RNN 的基础上，Encoder–Decoder 架构成为早期机器翻译等任务的主流范式。该架构试图将任意长度的输入序列编码为一个固定长度的向量，再由解码器生成输出。这种设计在工程上极具吸引力：接口统一、结构简洁，似乎也符合“一句话有一个整体含义”的直觉。

但这一设计隐含了一个极强的假设：序列中的所有关键信息都可以被无损压缩进一个固定维度的向量中。语言并不满足这一假设。自然语言包含多实体、多关系、多层次结构，将这些信息压缩为单一向量，必然带来信息丢失。

五、从 RNN 到 LSTM：为“记不住”而生的改造

随着 RNN 被用于更长的句子、更复杂的翻译与生成任务，人们发现一个反复出现的问题：模型很难稳定地保留长距离信息。训练中常见的现象包括梯度在长序列上逐步衰减或放大，导致早期输入对后期输出的影响越来越弱；同时，隐藏状态维度固定，使得历史信息被不断覆盖，重要但较早出现的内容容易丢失。

LSTM（以及后来的 GRU）正是在这一背景下提出的。它并不改变“用递归方式推进序列”的总体框架，而是对 RNN 的内部记忆结构做了加强：引入显式的记忆通道，并用门控机制控制信息的写入、保留与读取，从而使模型在训练上更容易保留较长时间跨度的关键信息。

然而，LSTM 仍然继承了 RNN 的结构性前提：所有历史信息最终仍要通过有限维度的状态来承载，并且信息的使用仍遵循顺序访问。也就是说，LSTM 能显著缓解“记不住”的训练困难，但并未从根本上改变“固定容量 + 顺序传递”的结构限制。

六、RNN 与 LSTM 的结构性瓶颈

RNN 与 LSTM 的第一个核心问题是表示容量受限。隐藏状态维度是固定的，而输入序列长度却可变且可能很长。随着序列增长，新信息不断进入，早期但重要的信息容易被覆盖，出现表示能力饱和的现象。

第二个问题是依赖路径过长。远距离依赖必须通过逐步状态传递来实现，依赖路径长度随序列长度线性增长。这使得信息需要经过多次非线性变换才能抵达目标位置，导致远距离信息逐渐被稀释；同时也加剧了训练中梯度不稳定的风险。

第三个问题是访问方式受限。无论是 RNN 还是 LSTM，当模型在某一步需要利用很早之前的某个 token 信息时，都无法直接读取那个位置的表示，只能依赖逐步传递后的“残留痕迹”。这使得模型很难做到“按需回看”，更谈不上对不同上下文进行灵活检索。

七、CNN 的引入：以并行与局部模式补足序列建模

在深度学习体系中，CNN 以并行计算效率高、善于捕捉局部模式而著称。将 CNN 引入序列建模的动机，主要来自两个现实需求：一是希望摆脱 RNN 的严格时间依赖，从而提升训练与推理的并行效率；二是希望利用卷积对局部 n-gram 结构的强归纳偏置，更高效地抽取短程组合模式。

在文本序列中，CNN 通常通过局部卷积提取短程特征，再通过堆叠多层扩大视野，以期覆盖更长距离的上下文。这种思路在一定程度上能兼顾速度与局部结构建模，因此一度成为与 RNN 并行发展的路线。

八、CNN 的“感受野”问题及其语言局限

所谓感受野，指网络中某个位置的表示最终能够“看到”的输入范围。在 CNN 中，单层卷积只能关注局部窗口，想要覆盖更远的距离，必须不断增加网络深度。于是出现了第一个问题：感受野增长缓慢，要覆盖整句往往需要非常深的网络。

更关键的是第二个问题：即使感受野在理论上覆盖了全句，远距离信息仍需要经过多层非线性变换才能传递到目标位置，路径长度与网络深度直接相关。距离越远，通常意味着需要更多层的传递，信息更容易在层层变换中衰减，远距离依赖的贡献被持续稀释。

此外，卷积窗口是固定的，它无法根据当前语义需求动态改变“该看谁”。语言中的关键依赖往往是稀疏且结构化的：当模型处理某个词时，它真正需要关注的可能是远处的某个主语或指代对象，而不是附近的若干词。CNN 的局部、固定窗口机制难以提供这种基于上下文的选择性访问能力。

九、长距离依赖：语言建模的本质矛盾

自然语言中的依赖关系具有三个显著特征：依赖在整体中是稀疏的，但一旦存在便至关重要；依赖的重要性并不随距离单调衰减，而由句法和语义结构决定；依赖是动态的，不同位置在不同上下文中需要关注不同的历史信息。

而 RNN、LSTM 与 CNN 的共同问题在于，它们都在用固定结构提前决定信息如何被压缩或传播：要么将历史压缩进有限维度的状态，要么通过局部堆叠被动扩大视野。这种结构假设与语言依赖的选择性与动态性存在根本冲突。

十、注意力机制：从“压缩历史”到“动态选择”

注意力机制的提出标志着序列建模思路的关键转向。与其将所有历史信息压缩进一个固定向量，注意力机制选择保留所有位置的中间表示，并在当前任务需要时，通过可学习的权重对历史信息进行加权选择。

在这种机制下，模型不再依赖单一记忆状态，而是根据当前上下文动态决定“该看谁、看多少”。注意力提供了一种可学习的软指针，使模型能够直接访问与当前预测最相关的部分，从而显著缩短了信息传递路径，并缓解了固定长度表示带来的信息瓶颈。

十一、Transformer：结构性转变的完成

Transformer 正是在注意力机制的基础上构建的。它彻底放弃了以时间步为核心的顺序递归结构，转而采用基于自注意力的全局依赖建模方式。在 Transformer 中，任意两个位置之间都可以直接建立联系，依赖路径长度不再随序列长度增长。

同时，由于不再依赖前一时间步的隐藏状态，Transformer 可以对所有位置并行计算注意力权重。这一特性使其在 GPU 上具备极高的计算效率，为大规模模型和海量数据训练提供了可行性。自注意力机制既实现了“保留所有信息”，又通过权重分配实现“按需选择”，从结构上更贴合语言依赖稀疏、动态且不随距离衰减的特性。

十二、总结

从词向量到序列模型，问题从“词如何用向量表示”逐步走向“词如何形成结构化语义”。RNN 用递归状态试图承载历史，LSTM 在此基础上通过门控增强记忆保留能力，CNN 以卷积堆叠的方式在并行效率与局部模式建模上提供替代路径。然而，它们共同面临的结构性限制是：要么依赖固定容量的压缩状态，要么依赖固定窗口与多层传递的被动传播，难以对语言中稀疏而关键的长距离依赖进行动态、直接的访问。

Transformer 的关键突破在于改变了这一前提：它不再提前压缩历史，而是保留所有位置的表示，通过自注意力为每个位置动态分配依赖权重，实现对关键信息的直接访问；同时，其计算天然支持并行，使得在大规模数据与算力条件下训练更深更大的模型成为可能。这种从“顺序传递”到“全局访问、动态选择”的结构转变，构成了序列建模范式演进的核心脉络。

十三、关键要点

1. 核心问题

自然语言的长距离依赖具有稀疏性、非单调性、动态性三大特征，这与传统序列模型的固定结构假设存在根本冲突。

2. 两种范式

压缩传递（RNN/LSTM）：将历史压缩进固定维度状态，像把整本书总结成一句话
选择访问（Transformer）：保留所有位置的完整表示，通过动态计算注意力权重决定“该看谁、看多少”，再加权提取信息——相当于保留整本书，每次根据需要重点阅读相关章节

3. 依赖路径

信息传递路径长度决定了远距离依赖的建模能力：RNN/LSTM 为，CNN 为至，Transformer 为。

4. 结构性瓶颈

RNN/LSTM：固定容量 vs. 可变序列 → 表示瓶颈
CNN：固定窗口 vs. 稀疏依赖 → 访问受限
Transformer：全局注意力 → 并行高效，但复杂度为

5. 范式转变

从“如何更好地压缩”（LSTM 的工程优化）到“是否需要压缩”（Attention 的结构创新），后者带来了序列建模的根本性突破。

从 One-hot 到 Embedding：词的分布式表示是如何从语料中学习得到的

发表于 2026-01-31

以下内容由AI辅助生成

在自然语言处理任务中，模型面对的基本对象是离散的符号（词或 token），而大多数机器学习方法只能处理连续数值。因此，一个核心问题是：如何将离散的词表示为数值向量，并使这些向量能够反映词的语义与用法差异。

词向量（word embedding）正是对这一问题的系统性回答。本文将从最基础的表示方法出发，逐步引入分布式表示与 embedding 的训练机制，并以 Skip-gram + Negative Sampling 为例，说明词向量是如何通过损失函数和梯度下降从大规模语料中学习得到的。

1. One-hot 表示：离散符号的直接编码

最直接的词表示方法是 one-hot 编码。

设词表大小为，则每个词对应一个维向量，仅在该词对应的位置为 1，其余位置为 0。例如，词表为：

$我爱你中国北京$

则“北京”的 one-hot 表示为：

one-hot 的优点在于形式简单、语义唯一、不需要训练；但其缺点同样明显：

向量维度随词表线性增长，难以扩展
表示高度稀疏，计算与存储效率低
不包含任何语义信息，不同词之间的相似度恒为 0

因此，one-hot 只能作为索引机制，而无法承担“语义表示”的角色。

2. 分布式表示的核心思想

2.1 分布式表示的基本假设

分布式表示（distributed representation）基于一个经典假设：

一个词的意义可以通过它的上下文分布来刻画。

在这一思想下，每个词不再由一个孤立的维度表示，而是由一个低维、稠密、连续的向量表示；语义相近的词，其向量在空间中也应当相近。

2.2 构建分布式表示的两类方法

构建词的分布式表示，主要有两大类方法：

基于计数的方法（count-based methods）
- 典型代表：LSA、基于共现矩阵的 SVD、PMI / PPMI
- 思路：先统计词与上下文的共现频次，再通过矩阵分解获得低维表示
- 特点：依赖全局统计，数学结构清晰，但在大规模语料上扩展性较差
基于神经网络的推理方法（prediction-based methods）
- 典型代表：Word2Vec（Skip-gram / CBOW）、GloVe（部分融合统计思想）
- 思路：将“学习词向量”转化为一个预测任务，通过最小化损失函数学习向量参数
- 特点：可在线训练、扩展性好、在实践中效果优异

本文后续讨论的 embedding 学习机制，属于第二类：基于神经网络的推理方法。

3. Embedding 的形式化定义

在神经网络框架中，embedding 可以形式化为一个可学习的查表映射：

词表大小：
向量维度：
embedding 矩阵：

对于任意一个词（或 token），embedding 层的作用可以理解为：
根据词的 id，从矩阵中取出对应的一行，作为该词的向量表示。

embedding 的参数并非人工设定，而是通过下游训练目标、借助梯度下降从数据中学习得到。

4. Skip-gram + Negative Sampling：从语料到训练目标

4.1 训练样本的构造

给定一个 token 序列：

设窗口大小为，对每个位置，构造训练对：

中心词：
上下文词：，其中

这样即可从原始语料中构造大量正样本对。

4.2 输入向量表与输出向量表

在 Skip-gram 模型中，会维护两张独立的 embedding 表：

输入向量表：用于中心词
输出向量表：用于上下文 / 候选词

对词表中任意词 id 为 i：

在输入向量表中，取到它作为“中心词”时使用的向量
在输出向量表中，取到它作为“候选上下文词”时使用的向量

这两种向量使用相同的词表索引，但参数彼此独立，承担的统计角色也不同。

4.3 打分函数与概率建模

在 Skip-gram 中，模型会为“中心词 + 候选词”这一对分配一个匹配分数。

这个分数可以理解为：
中心词向量与候选词向量在向量空间中的相似程度。

随后，模型会把这个分数映射成一个介于 0 和 1 之间的值，用来表示“该候选词是否真的是中心词上下文”的概率。

5. 损失函数与向量学习机制

5.1 Negative Sampling 的训练目标

对于一个真实的中心词–上下文词对，Negative Sampling 的训练目标可以分解为两点：

正样本目标
让中心词与真实上下文词的匹配分数变大。
负样本目标
随机采样若干个与无关的词作为负样本，
并让中心词与这些负样本的匹配分数变小。

训练时，模型会把“真实上下文”当作正类，“随机词”当作负类，
并对每一对样本计算二分类的对数损失，然后把这些损失加起来进行优化。

5.2 为什么一次更新会同时影响多种向量

需要强调的是：
输入向量和输出向量并不是分别训练的，而是由同一个训练目标同时驱动。

在一次训练中：

中心词对应的输入向量会被更新
真实上下文词对应的输出向量会被更新
每一个负样本对应的输出向量也都会被更新

从几何角度看，训练过程等价于：

把中心词向量与真实上下文向量在空间中拉近
把中心词向量与随机负样本向量在空间中推远

6. 为什么需要两张向量表

引入输入表与输出表的根本原因在于：同一个词在训练目标中承担了两种不同的功能：

作为中心词：用于生成一个中间表示，以预测周围词
作为候选词：用于与中心词表示进行匹配，判断是否为真实上下文

这两种角色在语言统计中并不对称。强制它们共享同一套参数，相当于引入了不必要的约束，会削弱模型对真实共现结构的拟合能力。

训练完成后，实践中通常仅使用输入向量表中的向量作为最终词向量表示，因为它更稳定地反映了词在语义空间中的位置。

7. 一个最小可跑的 PyTorch 示例（核心机制版）

下面给出一个极简的 Skip-gram + Negative Sampling 实现，仅保留核心机制：

输入 / 输出向量的分离
正负样本共同驱动参数更新

import torch
import torch.nn as nn
import torch.nn.functional as F

V, D = 3, 2   # 示例：吃 / 苹果 / 北京

class SGNS(nn.Module):
    def __init__(self):
        super().__init__()
        self.in_emb = nn.Embedding(V, D)
        self.out_emb = nn.Embedding(V, D)

    def forward(self, center, pos, neg):
        v = self.in_emb(center)
        u_pos = self.out_emb(pos)
        u_neg = self.out_emb(neg)

        pos_loss = -F.logsigmoid(torch.sum(v * u_pos, dim=1))
        neg_loss = -F.logsigmoid(-torch.sum(v * u_neg, dim=1))

        return (pos_loss + neg_loss).mean()

在这个示例中可以看到：

一个损失函数同时作用于多种向量
每一步更新只涉及当前样本用到的向量行

8. 总结

One-hot 只是离散索引，不包含语义
分布式表示的目标是用低维稠密向量刻画词的使用规律
分布式表示可以通过计数方法或基于神经网络的推理方法构建
Skip-gram + Negative Sampling 将词向量学习转化为正负样本的区分问题
同一个训练目标同时驱动输入向量与输出向量的学习
通过大量样本的迭代更新，词的语义结构自然在向量空间中形成

为什么点积太大会导致 Softmax 梯度问题，以及这个问题是如何被解决的

发表于 2026-01-30

以下内容由AI辅助生成

一、问题背景：我们到底在担心什么？

在 Transformer 的注意力机制中，有一个非常经典的公式：

很多人在第一次看到这个公式时都会产生疑问：

为什么注意力机制使用点积来计算相关性？
为什么点积之后要接一个 softmax？
最关键的是：为什么一定要除以？

如果只是把它当成论文中的经验公式，那么对注意力机制的理解仍然停留在表面。事实上，这个结构并不是为了“效果更好看”，而是为了解决一个在训练过程中非常具体、而且非常致命的问题。

二、softmax 的作用，以及它对输入尺度的敏感性

softmax 的定义如下：

它的作用是把一组实数打分映射为一个概率分布。但 softmax 有一个非常重要的性质：

softmax 对输入的整体尺度极其敏感

当输入数值较为温和时，softmax 会产生一个相对平滑的分布；而当输入整体变大时，softmax 的输出会迅速变得极端。

一个简单的数值例子

情况一：输入尺度适中

1 2	输入: z = [1, 0] 输出: softmax(z) ≈ [0.73, 0.27]

两个位置都有明显概率，模型仍然保留不确定性。

情况二：输入尺度变大

1 2	输入: z = [10, 0] 输出: softmax(z) ≈ [0.9999, 0.0001]

此时 softmax 的输出已经几乎等同于 one-hot 分布 [1, 0]。

这是因为指数函数会将线性差距放大为指数级差距，只要输入的整体尺度变大，softmax 的输出就会迅速向极端塌缩。

三、注意力分数为什么会天然变大：点积的统计性质

在注意力机制中，softmax 的输入来自查询向量和键向量的点积：

对于单个 query-key 对，这个分数可以写成：

在常见训练设置中（例如经过 LayerNorm 之后），可以合理假设：

各维度的相互独立
均值为 0
方差为 1

点积方差的数学推导

在上述假设下，对于每一项：

均值：
方差：

当项独立相加时：

因此标准差为：

关键结论：点积的典型数值规模与成正比

这并非实现细节或偶然现象，而是高维点积在统计意义上的必然结果。

具体数值示例

维度	点积标准差	典型点积范围
64	8	[-16, 16]
128	11.3	[-23, 23]
512	22.6	[-45, 45]

当时，点积值可能达到 ±45，这会让 softmax 严重饱和。

四、softmax 的梯度结构：什么是 Jacobian？

softmax 是一个向量到向量的函数：

输入：
输出：

当输入和输出都是向量时，需要描述这样一件事：

某一个输入分量发生微小变化，会如何影响所有输出分量

所有这些“偏导关系”组成的一整张表，称为 Jacobian 矩阵：

softmax 的 Jacobian 具体形式

对于 softmax，其 Jacobian 有明确的数学形式：

关键观察：

当（饱和状态）时，
当时，

梯度大小直接由输出概率本身控制

五、softmax 饱和：输出分布发生了什么变化

对比：适中尺度 vs 大尺度

输入尺度适中时（例如）：

位置:    1      2      3      4
输入:    2      1      0     -1
概率:  0.52   0.28   0.14   0.06

可视化:
位置 1: ██████████████████ (52%)
位置 2: ████████████ (28%)
位置 3: ██████ (14%)
位置 4: ██ (6%)

在这种状态下，多个位置都具有非零概率，输出对输入变化是敏感的。

输入尺度变大时（例如）：

位置:    1      2       3        4
输入:   20     10       0      -10
概率:  1.00   0.00    0.00     0.00

可视化:
位置 1: ████████████████████████████████ (≈100%)
位置 2: (≈0%)
位置 3: (≈0%)
位置 4: (≈0%)

此时，几乎所有概率质量都集中在单一位置，其余位置的概率被压缩到接近零。

这种从“平滑分布”到“极端分布”的转变，称为 softmax 饱和（saturation）。

六、梯度是如何在 softmax 处消失的

在反向传播中，梯度的传递遵循链式法则：

未饱和状态：梯度正常传播

反向传播路径：

Loss
  │ ∂L/∂s (来自上游)
  ↓
softmax
  │ ∂s/∂z ≈ [0.2, 0.3, 0.1, ...] (梯度有效)
  ↓
logits z
  │ ∂z/∂Q, ∂z/∂K (梯度继续传播)
  ↓
Q, K (参数可以更新)

饱和状态：梯度被截断

反向传播路径：

Loss
  │ ∂L/∂s (来自上游)
  ↓
softmax
  │ ∂s/∂z ≈ [0.00001, 0, 0, ...] (梯度几乎为0！)
  ↓
logits z
  │ ∂z/∂Q ≈ 0, ∂z/∂K ≈ 0 (梯度消失)
  ↓
Q, K (参数无法更新！)

梯度不是在网络深处逐层衰减的，而是在 softmax 这一层被直接截断的

这是一种发生位置非常明确的梯度消失问题。

七、从点积到梯度消失的完整因果链

将前面的所有环节串联起来，可以得到一条完整因果链：

高维点积统计性质
    ↓
点积方差 ∝ d_k
    ↓
点积值的典型尺度 ∝ √d_k
    ↓
softmax 输入整体变大
    ↓
指数函数放大差距
    ↓
softmax 输出趋向 one-hot 分布
    ↓
softmax Jacobian 中梯度项趋近于 0
    ↓
∂s/∂z ≈ 0 导致梯度截断
    ↓
Q、K 无法更新，注意力权重过早固定

问题的本质是：点积让 softmax 过早进入了饱和区间，从而导致梯度消失。

八、为什么这不是梯度爆炸问题

这一现象有时会被误认为是梯度爆炸，但两者在机制上完全不同。

梯度爆炸 vs 梯度消失对比

特征	梯度爆炸	本文讨论的问题
梯度大小	趋向无穷大	趋向零
发生原因	导数累乘 > 1	softmax 饱和导致 ∂s/∂z ≈ 0
数值稳定性	数值溢出	数值下溢
训练表现	参数震荡、NaN	参数停止更新

关键区别：

softmax 的梯度由其输出概率控制，具体形式为和。由于概率值，这些导数在数值上是有上界的，不可能随着输入增大而放大梯度。

softmax 只会压缩梯度，而不会放大梯度。

因此，这里出现的问题不是梯度失控增大，而是梯度被系统性压缩并最终消失。

九、根本解决方案：Scaled Dot-Product Attention

既然问题的根源在于点积的方差与维度成正比（），那么最直接的解决方式就是对点积进行缩放：

缩放后的统计性质

缩放后，点积的方差变为：

效果：

控制点积的典型尺度稳定在常数级别（与维度无关）
防止 softmax 过早进入饱和区
保持输出对输入变化的敏感性
让梯度能够持续传回 Q 和 K

这一步的本质是方差归一化（variance normalization）。

十、为什么是

三种缩放方式的对比

缩放方式	softmax 行为	问题
不做缩放	很快饱和	梯度消失
除以	过于均匀	区分能力不足，所有位置概率接近
除以	稳定且可学习	✓ 最优

直观解释

不做缩放：点积方差随线性增长，softmax 很快饱和
**除以 **：矫枉过正，点积方差变成，当很大时会让所有注意力权重过于平均，失去了“注意”的意义
**除以 **：恰好让方差归一化到 1，既不会饱和也不会过于平滑

这一选择与 Xavier 初始化、LayerNorm 等方法背后的统计思想是一致的：保持信号的方差在网络中稳定传播。

十一、总结

点积过大不会导致梯度爆炸，而是会使 softmax 过早进入饱和状态。一旦 softmax 的输出分布变得极端，其 Jacobian 中的梯度项会趋近于零，导致梯度在这一层被有效截断，学习信号无法继续传播到 Q 和 K。

的引入，正是为了把点积的方差从归一化到 1，从而把 softmax 的输入尺度拉回到一个模型仍然能够持续学习的区间。

这是一个精心设计的数学解决方案，背后的统计原理清晰明确。

残差连接（Residual Connection）：从直觉困境到现代神经网络的核心结构

发表于 2026-01-30

以下内容由AI辅助生成

1. 引言：一个看似显然却失败的直觉

在深度学习中，一个最自然的想法是：

神经网络越深，模型的表达能力越强，性能应该越好。

然而，大量实验表明，当网络深度不断增加时（例如从几十层到上百层），模型往往会出现一个反直觉现象：

训练误差上升
即使在训练集上，也无法达到较浅网络的性能

这种现象被称为深层网络退化问题（Degradation Problem）。

重要的是，这并不是由于过拟合，也不仅仅是梯度消失或爆炸，而是一个深层模型在优化层面“学不动”的问题。

2. 问题的本质：为什么深层网络会“退化”？

从理论上看，一个更深的网络至少应该能够模拟一个浅层网络：

只要新增的层学会恒等映射（Identity Mapping）
网络性能就不应下降

但实践中发现：

普通神经网络并不擅长学习“恒等变换”

也就是说，让几层网络保持输出与输入一致（y = x），在数值优化上并不容易。

这揭示了退化问题的本质：

不是模型不够强
而是优化目标本身不友好

3. 残差连接的直观思想

残差连接的核心思想可以用一个非常生活化的比喻来理解。

传统网络：

从零开始学习一个完整映射
残差思想：

在原有输入的基础上，只学习“需要修正的部分”

换句话说，与其直接学习目标函数，不如学习它相对于输入的偏差。

4. 形式化定义：什么是残差连接？

在数学上，残差学习通过一次重参数化来实现。

传统形式：

残差形式：

其中：

：输入
：残差函数
从直接加到输出的通路称为 残差连接（Residual / Skip Connection）

5. 为什么残差连接有效？

5.1 恒等映射变得容易

如果某些层对任务无贡献：

普通网络：很难逼近恒等映射
残差网络：只需令

这使得：

“零修正”成为一种稳定解

从而保证深层网络至少不会比浅层网络更差。

5.2 梯度传播更顺畅

对于残差结构：

反向传播时：

这个恒定的 “+1”：

为梯度提供了一条直接通路
显著缓解了梯度消失问题

5.3 优化过程更友好

经验和理论分析表明：

残差结构使损失函数的优化景观更加平滑
梯度下降类方法更容易收敛

这是极深网络得以成功训练的关键。

6. 一个重要澄清：是不是每一层都应该用残差？

答案是否定的。

现代神经网络并不是对每一层使用残差，而是：

在“模块（Block）级别”使用残差连接

原因在于：

层层残差会削弱非线性表达能力
有些层的目标是“改变表示空间”，并不适合残差

7. 残差连接在经典模型中的使用

7.1 ResNet

ResNet 的基本单元不是单层，而是一个残差块：

2～3 层卷积 + 非线性
外部包裹一条 shortcut

残差连接作用于整个模块，而非每一层。

7.2 Transformer

在 Transformer 中：

Attention 子层
Feed-Forward 子层

每一个子层外部都配有残差连接，但子层内部仍然是传统结构。

这说明：

残差是一种结构设计原则，而不是具体算子。

8. 什么时候不适合使用残差连接？

通常不使用残差的地方包括：

输入嵌入层
下采样或维度剧烈变化的层
输出层（分类 / 回归头）
非常浅的网络

残差更适合用于：

在同一表示空间内逐步精炼特征

9. 总结

残差连接的核心价值在于：

重参数化学习目标，使优化更容易
为梯度提供稳定通路
保证深层模型不发生性能退化

因此，现代深度学习模型的设计范式可以概括为：

用传统网络层构建表示，用残差连接保证这些表示能被有效优化。

这也是为什么，从 ResNet 到 Transformer，残差连接已经成为深度模型的基础组件。

从 0 理解梯度消失与梯度爆炸

发表于 2026-01-30

以下内容由AI辅助生成

一、训练神经网络到底在做什么

训练神经网络,本质只有一件事:

不断微调参数,使模型输出更接近真实目标。

参数该往哪个方向调、调多大力度,完全由梯度决定。

如果梯度能够稳定传播,模型就能学习;
如果梯度在传播过程中衰减或失控,训练就会失败。

二、什么是梯度(不涉及神经网络)

1. 变化率的直觉理解

考虑函数:

当发生微小变化时, 的变化量取决于当前位置。

在附近, 增加 0.01, 约增加 0.02
在附近,同样增加 0.01, 却增加约 0.2

这说明:
同样的输入变化,在不同位置,对输出的影响不同。

2. 导数的定义

这种“对变化的敏感程度”,就是导数。

数学上,导数的定义为:

对 :

注: 在单变量函数中称为导数,在多变量函数中,所有偏导数组成的向量称为梯度。

三、梯度在训练中的作用

1. 参数是如何被更新的

设一个最简单的模型:

定义损失函数:

训练的目标是让损失变小。

2. 梯度下降规则

参数更新公式为:

其含义是:

梯度大 → 参数调整幅度大
梯度小 → 参数调整幅度小
梯度为 0 → 参数不再更新

梯度决定了模型是否还能继续学习。

四、神经网络中的梯度从哪里来

1. 神经网络是复合函数

多层神经网络可以表示为函数嵌套:

损失函数是。

2. 反向传播的本质

反向传播使用链式法则计算梯度:

也就是说:

梯度是多个导数的连乘结果。

五、梯度消失:为什么“传不到前面”

1. 连乘导致的数值衰减

假设每一层反向传播的导数约为 0.5:

10 层:
50 层:

梯度几乎为 0。

2. 对训练的影响

输出层附近仍能更新
输入层附近梯度趋近于 0
参数几乎不发生变化

这称为梯度消失(Vanishing Gradient)。

六、梯度爆炸:同一机制的反面

1. 连乘导致的数值放大

若每一层导数约为 1.5:

10 层:
50 层:

2. 对训练的影响

参数更新幅度极大
损失函数变为 NaN 或 inf
数值溢出,模型发散

这称为梯度爆炸(Exploding Gradient)。

七、激活函数为什么会深刻影响梯度

1. 激活函数的作用

如果每一层只有线性变换:

多层叠加后仍等价于一次线性变换,模型表达能力有限。

因此神经网络必须引入非线性激活函数。

2. 激活函数在反向传播中的角色

在反向传播过程中,每一层梯度都会乘上激活函数的导数:

$梯度$

激活函数的导数直接决定梯度是被缩小,还是能够稳定传播。

3. Sigmoid:典型的饱和型激活函数

函数形态:

y
1 |           ________
  |         /
  |       /
0 |______/____________ x
  -∞   0         +∞

形态特征:

输出值域在 (0, 1) 之间
两端逐渐变平,存在明显饱和区
当输入绝对值较大时(如或 ),函数几乎不变化
在饱和区内,导数接近 0
最大导数出现在处,值为 0.25

多层连乘后,即使在最佳位置,导数也只有 0.25,梯度迅速衰减,极易出现梯度消失。

4. ReLU:非饱和激活函数

函数形态:

y
  |
  |        /
  |       /
0 |______/____________ x
  -∞   0         +∞

形态特征:

负区间输出恒为 0( 时 )
正区间保持线性增长( 时 )
正区间内导数恒为 1
负区间内导数恒为 0

优点: 梯度在正区间不会被缩小,更适合深层网络。

缺点: 负区间梯度为 0,可能导致“神经元死亡”问题(Dead ReLU),即某些神经元永远不会被激活。

5. GELU:平滑的非饱和激活函数

函数形态:

y
  |          /
  |        /
  |     __/
0 |____/______________ x
  -∞   0         +∞

形态特征:

整体趋势类似 ReLU
负区间平滑过渡,而非硬截断(允许小的负值通过)
在附近是光滑可导的
同时保持梯度稳定与函数连续性
避免了 ReLU 的“神经元死亡”问题

因此在 Transformer 等现代深层模型中被广泛采用。

6. 激活函数对梯度的整体影响

Sigmoid / Tanh: 饱和型激活函数,导数最大值为 0.25(Sigmoid)或 1(Tanh),在饱和区导数接近 0,易导致梯度消失
ReLU: 非饱和激活函数,正区间导数恒为 1,但负区间导数为 0,可能导致神经元死亡
GELU / Swish: 平滑的非饱和激活函数,结合了 ReLU 的优点并避免了硬截断,在深层网络中表现更好

八、梯度消失与爆炸的本质

梯度问题并非偶然,而是反向传播机制的必然结果:

小于 1 的数反复相乘 → 梯度消失
大于 1 的数反复相乘 → 梯度爆炸

问题与网络深度、激活函数和结构设计强相关。

九、常见解决思路

针对梯度消失:

使用非饱和激活函数(如 ReLU、GELU)代替 Sigmoid、Tanh
引入残差连接(ResNet),为梯度提供直接的反向传播路径
使用批归一化(Batch Normalization)或层归一化(Layer Normalization)稳定数值尺度
适当的权重初始化(如 Xavier、He 初始化)使初始梯度保持在合理范围

针对梯度爆炸:

梯度裁剪(Gradient Clipping),限制梯度的最大范数
降低学习率
使用权重正则化(如 L2 正则化)
批归一化同样有助于防止梯度爆炸

十、总结

梯度消失是信号衰减问题,
梯度爆炸是信号放大失控问题。

深度学习模型结构的演进,本质上是在解决同一个问题:
如何让梯度稳定、完整地传回去。

链式法则与反向传播：从直觉到结构理解

发表于 2026-01-30

以下内容由AI辅助生成

本文从导数的直觉含义出发，逐步引入链式法则、偏导数、反向传播与梯度下降，并通过一个带分叉的完整计算图示例，解释反向传播为什么必须存在，以及梯度复用与梯度汇总在计算中究竟发生在什么地方。

一、导数的本质：变化率

导数描述的是变量之间的变化关系：

当一个量发生微小变化时，另一个量会随之变化多少。

数学上通常写作：

直觉上可以理解为：

每增加一点点，大概会增加或减少多少。

在机器学习中，导数的意义并不是求解数学问题，而是用于判断如何调整参数，结果才会向更好的方向变化。

二、多变量函数与偏导数

实际问题中，函数往往依赖多个变量，例如：

此时，单一导数已经不足以描述不同变量对结果的影响。偏导数的含义是：

在保持其他变量不变的前提下，只考察某一个变量变化，对结果造成的影响。

例如：

则有：

即使是同一个损失函数，不同参数对它的影响程度也是不同的。

三、多步计算与链式法则

当一个量的变化需要通过中间变量传递时，就会出现多步依赖关系。

设：

则：

这就是链式法则。

它的直觉表述是：

多步计算的变化率，可以拆成每一步变化率的连乘。

链式法则是反向传播的核心数学规则，但并非唯一规则。在分叉结构中，还需要偏导数的加法规则来汇总来自不同路径的梯度。

四、神经网络的数学本质

从数学角度看，神经网络只是一个参数极多、结构复杂的函数：

训练的目标可以概括为一句话：

通过调整参数，使损失函数尽可能小。

关键问题因此变成：

每个参数改变一点点，会让损失函数变多少？

也就是计算：

五、正向传播与反向传播的分工

正向传播的作用是计算数值。

在正向传播中，输入数据沿着计算图向前传递：

$中间变量$

在一次正向传播完成后，损失函数是一个确定的数值。

反向传播并不是将函数倒过来计算，而是：

在正向计算完成之后，以损失函数为起点，沿计算图的反方向系统地应用链式法则，计算损失函数对各个中间变量和参数的偏导数。

反向传播过程中传递的不是损失函数本身，而是：

$当前变量$

也就是说，如果当前位置发生单位变化，最终损失函数会变化多少。

六、梯度下降：参数更新发生的地方

反向传播的结果是得到各个参数对应的梯度，但它本身并不修改参数。

参数的更新由梯度下降完成：

其中，是学习率，用来控制每一步更新的幅度。

梯度的符号决定更新方向，梯度的大小决定更新步长。当梯度逐渐接近零时，参数逐步逼近损失函数的极小值。

七、为什么反向传播要沿着计算图反向进行

在线性链结构中，每个节点只有一条梯度传播路径，反向传播的优势不太明显。

真正的区别来自具有分叉和汇合的结构。

在分叉结构中，一个节点可能同时影响多个下游节点；在反向传播时，这些下游节点对损失函数的影响，必须被完整地汇总回上游节点。这一过程无法通过简单的正向计算完成。

因此，反向传播在工程上是不可替代的。

八、一个完整的二分叉数值示例

计算图结构

            h2 = w2 · h1
          ↗
x ──→ h1                ──→ y = h2 + h3 ──→ L
          ↘
            h3 = w3 · h1

对应的数学定义为：

设定具体数值：

正向传播计算过程

此时，损失函数是一个确定的数值。

反向传播计算过程

现在从损失函数开始，逐步计算每个变量的梯度。

第一步：计算

第二步：梯度分发到两个分支

由于，梯度会同时传递到两个分支：

第三步：计算和

第四步：梯度汇总到

这是关键步骤。由于同时影响和，来自两个分支的梯度必须相加：

第五步：计算

至此，我们得到了所有参数的梯度：

九、反向传播在分叉结构中的作用方式

反向传播仍然完全遵循链式法则。差异不在于数学规则本身，而在于计算图的结构。

在上述分叉结构中：

输出同时依赖于和，因此损失函数对的梯度会被同时传递到这两个分支。这是梯度分发。

中间节点同时影响和，因此在反向传播时，来自不同分支的梯度必须在处进行相加。这是梯度汇总，遵循偏导数的加法规则。

此外，正向传播中计算得到的中间变量（如）会在反向传播中被多次使用（计算和时都用到了），从而避免重复计算。这是梯度复用。

这些现象并不是额外引入的规则，而是链式法则和偏导数加法规则在分叉计算图中的自然结果。

十、总结

导数描述变量之间的变化率，偏导数用于区分多变量函数中不同变量的影响。链式法则解决多步依赖问题，偏导数的加法规则处理梯度汇总。反向传播是以损失函数为起点，对这些数学规则在计算图上的系统组织。梯度下降利用反向传播得到的梯度更新参数。在具有分叉结构的网络中，反向传播天然包含梯度分发、梯度复用与梯度汇总。

可以用一句话概括全文：

反向传播不是新的数学，而是对链式法则和偏导数加法规则在复杂计算图上的高效组织与实现。

感知机与神经网络如何学习并逼近复杂函数

发表于 2026-01-30

以下内容由AI辅助生成

——从函数形式到分段线性逼近的机制说明

一、感知机与神经网络的基本函数形式

在深度学习中，感知机及其扩展的神经网络，并不是在使用人为指定的多项式函数形式，例如：

其基本计算结构为：

其中：

：输入特征
：可学习参数
：激活函数（形式固定，由模型结构决定）

神经网络的非线性能力并非来自显式写入平方、立方项，而是来自激活函数与多层组合。

二、模型结构与参数学习的区分

神经网络需要在两个层面上理解：

结构层面：
层数、连接方式、激活函数类型（人为设计）
参数层面：
权重、偏置（通过数据训练得到）

网络不会“选择一个解析公式”，而是在固定结构下，通过参数不断调整，形成某种函数形状。

三、单层感知机的表达能力边界

当模型只有一层（无隐藏层）时：

虽然激活函数引入了非线性，但其表达能力仍然受限：

决策边界是线性的（对于分类任务）
无法表示真正复杂的非线性决策区域

例如 XOR、圆形边界等问题，无法由单层感知机解决。
复杂函数的表达能力来自隐藏层。

四、复杂函数是如何被“学出来”的

神经网络学习复杂函数的过程，本质是连续的数值优化：

参数随机初始化，函数形状与目标无关
前向传播，计算当前模型对应的输出函数
计算损失函数，仅反映预测误差
反向传播，计算参数对损失的梯度
梯度下降，微小更新参数
多次迭代，函数形状逐步调整

模型并不“理解函数形式”，只是不断在函数空间中朝误差更小的方向移动。

五、非线性激活的作用（以 ReLU 为说明示例）

为便于几何化理解，引入 ReLU 激活函数作为示例：

对一维输入：

其几何特征为：

当，输出为 0
当，输出为一条直线

一个 ReLU 神经元在一维输入下，只做一件事：
在某个位置之后，开始贡献一段线性函数。

六、折点的定义与来源

ReLU 的“折点”定义为：

需要明确：

网络中不存在名为的独立参数
折点是权重与偏置的比值结果
训练过程中仅对做梯度下降
折点位置是参数学习的自然副产物

七、多 ReLU 网络的函数性质

对一维输入、单隐藏层 ReLU 网络：

该函数族具有严格性质：

在任意区间内是线性的
在折点处一阶导数发生跳变
整体函数为分段线性函数

复杂性来自多个折点及其线性部分的叠加。

八、三 ReLU 拼接示例（严格区分“折点”与“输出折线”）

考虑如下网络：

1. 折点（竖直分界线）

该网络包含三个 ReLU，因此理论上只有三个折点：

它们对应三条竖直分界线，用于划分输入区间，本身不是函数图像的一部分：

1 2	│ │ │ t₁ t₂ t₃

2. 区间划分

折点将输入轴划分为四个区间：

3. 各区间内的函数来源（这是关键）

区间 A：

ReLU(x+1) = 0
ReLU(x) = 0
ReLU(x−1) = 0

输出为：

这是一个常数函数，因此图像是一条横线。

这条横线并不对应任何单个 ReLU
而是“三个 ReLU 全部未激活”的叠加结果

区间 B：

ReLU(x+1) = x+1
其余两个 ReLU = 0

输出为：

这一段直线由 ReLU₁ 单独贡献

区间 C：

ReLU(x+1) = x+1
ReLU(x) = x

输出为：

这一段直线是 ReLU₁ 与 ReLU₂ 的线性叠加

区间 D：

三个 ReLU 全部激活

输出为：

这一段直线是 三个 ReLU 的线性部分之和

4. 输出函数的折线示意（结果）

y
│               /
│            __/   ← ReLU₁ + ReLU₂ + ReLU₃
│         __/
│      __/        ← ReLU₁ + ReLU₂
│   __/
│__/              ← ReLU₁
│──────────────   ← 所有 ReLU = 0（常数段）
└──────────────── x
   -1     0     1

需要严格理解：

竖线（t）：表示 ReLU 的激活边界
折线：表示当前所有“已激活 ReLU”的线性部分之和
折线不是某个 ReLU 单独“画出来的”

九、为什么这种结构可以逼近抛物线

抛物线的本质特征是：

斜率随连续增大

ReLU 网络无法产生连续曲率，但可以通过：

足够多折点
足够密的斜率跳变

在有限区间内逼近这种行为。

十、有限 ReLU 的表达极限

在一维情况下：

有限 ReLU 网络 ⇒ 分段线性函数
⇒ 处处光滑、二阶导数非零

因此：

❌ 有限 ReLU 无法在整个实数轴上精确等于
✅ 在任意有限区间内，可以逼近到任意精度

十一、需要多少个 ReLU（量级结论）

在区间上，用单隐藏层 ReLU 网络逼近：

若最大误差为，所需 ReLU 数量满足：

含义为：

区间越大 → 折点越多
精度要求越高 → 折点越多

十二、整体总结

神经网络不显式构造高次多项式
表达能力来自线性变换与非线性激活的组合
ReLU 在一维下本质生成分段线性函数
折点是参数学习的自然结果，而非人为设定
折线是多个 ReLU 线性部分的叠加结果
光滑函数只能被有限 ReLU 逼近，不能被精确等同

交叉熵损失与最大似然估计：完全理解指南

发表于 2026-01-29

以下内容由AI辅助生成

一、从最基本的问题开始

1.1 模型如何表达预测？

假设你在训练一个图像分类模型：

任务：判断这张图是「猫」还是「狗」？

模型不会直接给出“猫”或“狗”这样的硬答案，而是输出概率分布：

“我认为是猫的概率是 0.8，是狗的概率是 0.2”

👉 核心理解：模型输出的是“置信度（概率）”，而不是确定的答案。

1.2 如何评价模型预测的好坏？

假设真实答案是「猫」，我们看不同预测的质量：

模型给猫的概率 p	评价	期望的损失
0.99	非常准确	应该很小
0.8	比较好	适中
0.51	勉强对	较大
0.1	完全错误	应该很大

我们需要设计一个损失函数，满足：

正确答案的概率越大 → 损失越小
正确答案的概率越小 → 损失越大

1.3 为什么选择对数函数？

观察函数 loss = -log(p) 的行为：

正确类概率 p	-log(p)	含义
0.99	0.01	几乎完美
0.9	0.10	很好
0.5	0.69	随机猜测水平
0.1	2.30	很差
0.01	4.60	完全错误

关键特性：

p 接近 1 → 损失接近 0（奖励正确预测）
p 接近 0 → 损失趋向无穷（严厉惩罚错误）
非线性增长：从 p=0.9 到 p=0.1，损失增加了 20 倍以上

为什么对数函数如此合适？这来自最大似然估计的数学原理（第四章详解）。

1.4 交叉熵的最简形式

对于单次预测：

真实答案是类别 A
模型给 A 的概率是 p

损失函数：

这就是交叉熵的核心。

二、为什么叫“交叉熵”？

2.1 先理解“熵”

熵（Entropy）是信息论中的核心概念，衡量不确定性。

两个例子

例子 1：完全确定

明天 100% 会下雨
熵 = 0（无不确定性）

例子 2：完全随机

抛硬币，正反各 50%
熵最大（最大不确定性）

数学定义

对于概率分布 P：

含义：平均每次需要多少信息量（比特）来描述发生的事情。

2.2 什么是“交叉”？

现实中经常出现这种情况：

真实世界：按分布 P 在运行
你的认知：却认为它是分布 Q

当你用错误的分布 Q 去理解真实分布 P 时，会产生额外的“信息代价”。

交叉熵的定义

2.3 为什么叫“交叉”？

看公式的结构：

公式部分	来源	含义
P(x)	真实分布 P	事件实际发生的频率（权重）
log Q(x)	模型分布 Q	用模型的方式编码

“交叉”的含义：两个不同分布的交叉使用

权重来自 P
编码来自 Q

对比：

**熵 H(P)**：用自己编码自己
**交叉熵 H(P,Q)**：用别人编码自己

2.4 在机器学习中的应用

真实标签（one-hot）：P = [0, 0, 1, 0] — 第3类是正确答案

模型输出（Softmax）：Q = [0.1, 0.2, 0.6, 0.1]

计算交叉熵：

2.5 为什么简化成了 -log(p)？

在分类任务中，真实标签是 one-hot：只有正确类是1，其他是0

代入交叉熵公式，求和后只剩下正确类别那一项：

$正确类$

这就是为什么实际代码中：

1	loss = -log(Q[y_true])

三、二分类和多分类的具体形式

3.1 二分类交叉熵（Binary Cross Entropy）

设定：

模型输出：p = P(y=1|x)，通过 Sigmoid 得到
真实标签：y ∈ {0, 1}

损失函数：

理解：这是分段函数的简洁写法

真实标签 y	实际计算
y = 1	-log(p)
y = 0	-log(1-p)

具体例子：

真实标签 y = 1, 模型预测 p = 0.9
损失 = -log(0.9) ≈ 0.105

真实标签 y = 1, 模型预测 p = 0.1
损失 = -log(0.1) ≈ 2.303

3.2 多分类交叉熵（Categorical Cross Entropy）

完整流程：

步骤1：模型输出 logits

1	z = [2.0, 1.0, 0.1]

步骤2：Softmax 归一化

计算结果：p₁ ≈ 0.659, p₂ ≈ 0.242, p₃ ≈ 0.099

步骤3：计算交叉熵

真实标签 y = [0, 1, 0]（第2类是正确答案）

简化形式（利用 one-hot）：

四、从最大似然估计理解交叉熵

4.1 一个侦探问题

你发现了一枚硬币和抛掷记录：

1	结果：正、正、反、正、正

任务：判断硬币正面的概率是多少？

思考过程：

假设的概率 θ	出现这串结果的概率
θ = 0.5	0.5⁴ × 0.5¹ = 0.03125
θ = 0.8	0.8⁴ × 0.2¹ ≈ 0.0819
θ = 0.9	0.9⁴ × 0.1¹ ≈ 0.0656

结论：θ = 0.8 最能解释观测数据！

这就是最大似然估计（MLE）的核心思想。

4.2 概率 vs 似然：关键区别

概率（Probability）

已知：参数 θ
求：数据出现的概率
方向：从原因推结果

1	P(data\|θ) = “给定硬币特性，某个结果出现的概率”

似然（Likelihood）

已知：数据（已经发生了）
求：哪个参数最可能
方向：从结果推原因

1	L(θ\|data) = “给定观测结果，哪个参数最合理”

数学关系：L(θ|data) = P(data|θ)

数值相同，但含义完全相反。

4.3 硬币问题的形式化

Step 1: 建立概率模型

1 2	P(x=1\|θ) = θ # 正面 P(x=0\|θ) = 1-θ # 反面

Step 2: 计算联合概率

观测：正、正、反、正、正

假设独立：

Step 3: 似然函数

问题：θ 取什么值时，L(θ) 最大？

4.4 为什么要取对数？

这是连接 MLE 和交叉熵的关键步骤。

原因1：连乘变连加

对于 N 个样本：L(θ) = ∏ P(xᵢ|θ)

当 N 很大时：

数值下溢：太多小于1的数相乘，结果趋近0
计算困难：浮点数精度问题

取对数后：

连乘变连加，数值稳定！

原因2：不改变最优解

log 是严格单调递增函数：

原因3：求导更简单

原函数：L(θ) = θ⁴(1-θ)
对数函数：ℓ(θ) = 4log θ + log(1-θ)

求导：dℓ/dθ = 4/θ - 1/(1-θ) = 0

解得：θ = 0.8

4.5 MLE 的通用形式

给定：

数据：x₁, x₂, …, xₙ
参数：θ
模型：P(x|θ)

三步曲：

似然函数：L(θ) = ∏ᵢ P(xᵢ|θ)
对数似然：ℓ(θ) = ∑ᵢ log P(xᵢ|θ)
最大化：θ̂ = argmax ∑ᵢ log P(xᵢ|θ)

核心思想：

找一个参数 θ，使得“已发生的数据”在该模型下出现的概率最大。

4.6 从 MLE 到机器学习

监督学习中：

数据：(x₁,y₁), (x₂,y₂), …, (xₙ,yₙ)
模型：P_θ(y|x)

MLE 目标：

从最大化到最小化：

深度学习框架做最小化（梯度下降）：

右边就是负对数似然（NLL）

每个样本的损失：

这正是交叉熵损失！

五、MLE = NLL = 交叉熵

5.1 完整的等价链

最大似然估计（MLE）
    ↓ 取对数
对数似然（Log-Likelihood）
    ↓ 变号（max → min）
负对数似然（NLL）
    ↓ 用分布语言重写
交叉熵（Cross Entropy）

5.2 逐步推导

Step 1: MLE 原始形式

Step 2: 取对数

这是对数似然（Log-Likelihood）

Step 3: 变号

这是负对数似然（NLL）

Step 4: 用分布语言重写

真实分布 P（one-hot）：P(y|x) = 1 当 y=y_true，否则 = 0

模型分布：Q_θ(y|x) = P_θ(y|x)

交叉熵定义：

代入 one-hot：

与 NLL 完全一致！

5.3 核心等价关系

$交叉熵负对数似然（）$

因此：

$交叉熵对数似然最大似然估计$

5.4 为什么有不同的名字？

视角	术语	来源	强调什么
统计学	最大似然/对数似然	统计学	参数估计
信息论	交叉熵	信息论	分布差异
工程	NLL/CrossEntropyLoss	深度学习	损失函数

本质相同，只是不同学科的不同表述。

5.5 数值例子：三者的一致性

3分类问题，3个样本：

数据：

样本1: y₁=0, 预测 P_θ(0|x₁) = 0.7
样本2: y₂=1, 预测 P_θ(1|x₂) = 0.8
样本3: y₃=2, 预测 P_θ(2|x₃) = 0.5

方法1：MLE（最大化似然）

1 2	L(θ) = 0.7 × 0.8 × 0.5 = 0.28 log L(θ) = log(0.7) + log(0.8) + log(0.5) = -1.273

方法2：NLL（最小化负对数似然）

1	NLL = -log L(θ) = 1.273

方法3：交叉熵

L₁ = -log(0.7) ≈ 0.357
L₂ = -log(0.8) ≈ 0.223
L₃ = -log(0.5) ≈ 0.693
总和 = 1.273

三种方法，完全相同的结果！

六、为什么这样设计？

6.1 理论基础：来自统计学

分类模型在建模条件概率 P(y|x)

统计学告诉我们：

最自然的参数估计方法是 MLE
MLE 具有一致性、渐近正态性等优良性质
MLE 等价于最小化交叉熵

结论：

交叉熵不是人为设计的，而是从统计学基本原理推导出来的

6.2 工程优势：梯度简洁

Softmax + Cross Entropy 的梯度：

特点：

形式极简：就是预测值和真实值的差
没有复杂的链式法则
数值稳定：不会梯度消失或爆炸
计算高效

这就是为什么深度学习框架直接提供 CrossEntropyLoss。

6.3 信息论视角：最小化分布差异

交叉熵可以分解为：

其中：

H(P)：真实分布的熵（常数）
KL(P‖Q)：KL散度（分布差异）

因此：最小化交叉熵 ⟺ 最小化 KL 散度 ⟺ 让模型分布逼近真实分布

七、总结

7.1 核心理解

交叉熵损失 = -log(正确答案的概率)

= 负对数似然
= 最大似然估计的优化目标

7.2 从三个角度理解

直觉：

“你给正确答案分配的概率有多低，我就罚你多狠”

统计学：

“让已发生的数据在当前模型下概率最大”

信息论：

“用模型的分布去理解真实分布所付出的代价”

7.3 关键等价关系

$最大似然负对数似然交叉熵$

7.4 理解路径

1. 问题：如何评价模型预测？
       ↓
2. 直觉：正确答案概率越高越好
       ↓
3. 函数：-log(p) 提供合适的惩罚
       ↓
4. 统计学：这是最大似然估计
       ↓
5. 信息论：这也是交叉熵
       ↓
6. 等价：MLE = Log-Likelihood = NLL = Cross Entropy

7.5 最小记忆单元

如果只记一件事：

交叉熵 = -log(正确类的概率)

它来自最大似然估计：让模型给真实答案的概率最大

八、结语

交叉熵损失看似简单的 **-log(p)**，实际上：

来自统计学：最大似然估计的自然结果
来自信息论：分布差异的度量
工程优良：梯度简洁、数值稳定

理解交叉熵和最大似然的联系，你就真正理解了：

为什么这样设计损失函数
为什么深度学习能够工作
如何从原理出发思考问题